Escrita escondida
Criptografia - Parte II
Durante séculos, a cifra simples de substituição monoalfabetica — apresentada na edição anterior — foi suficiente para garantir o sigilo. Porém, o desenvolvimento continuado da análise de frequências destruiu a sua segurança. Era necessário, então, desenvolver uma nova cifra e mais forte.
Quadrado de Vigenère
 Blaise de Vigenère (1523 - 1596), um diplomata francês,
interessou-se pela Criptografia durante uma missão a Roma, onde encontrara
trabalhos de criptólogos. Em 1570 dedica-se a tempo inteiro a este seu novo
passatempo, publicando, dez anos mais tarde, o livro intitulado Traictè de Chiffres (Tratado de Cifras).
Neste, Vigenère apresenta vários temas; em especial, a encriptação através do
seu Quadrado de Vigenère, (quadro 1) — a nova geração de cifras por
substituição polialfabética. Este método utiliza 26 alfabetos de cifra para
codificar uma mensagem: o emissor encripta a primeira letra de acordo com um
alfabeto, a segunda letra por outro alfabeto, e assim em diante. Para
descodificar a mensagem é necessária a mesma palavra-chave de encriptação.
Blaise de Vigenère (1523 - 1596), um diplomata francês,
interessou-se pela Criptografia durante uma missão a Roma, onde encontrara
trabalhos de criptólogos. Em 1570 dedica-se a tempo inteiro a este seu novo
passatempo, publicando, dez anos mais tarde, o livro intitulado Traictè de Chiffres (Tratado de Cifras).
Neste, Vigenère apresenta vários temas; em especial, a encriptação através do
seu Quadrado de Vigenère, (quadro 1) — a nova geração de cifras por
substituição polialfabética. Este método utiliza 26 alfabetos de cifra para
codificar uma mensagem: o emissor encripta a primeira letra de acordo com um
alfabeto, a segunda letra por outro alfabeto, e assim em diante. Para
descodificar a mensagem é necessária a mesma palavra-chave de encriptação.
Eis um exemplo, para melhor percepção:
Mensagem a encriptar: A sua bela espada
é ferrugem.
Palavra-chave: cavaleiro
Palavra-chave: Texto simples: Texto cifra: |
C A V A L E I R O C A V A L E I R O C A V A L E I R
|
Para encriptares a primeira letra a, começas por identificar a letra-chave (da palavra-chave) correspondente: C. Esta letra define o alfabeto cifra a ser utilizado — este encontra-se na linha 2 do Quadrado de Vigenère. Assim, seguindo a coluna a, encontras a letra cifrada C. A letra-chave de s é A, definindo a linha 26. Na coluna s encontras S. Se continuares, obténs a mensagem cifrada.
Quadro 1 – Quadrado de Vigenère
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | |
| 1 | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A |
| 2 | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B |
| 3 | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C |
| 4 | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D |
| 5 | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E |
| 6 | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F |
| 7 | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G |
| 8 | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H |
| 9 | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I |
| 10 | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J |
| 11 | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K |
| 12 | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L |
| 13 | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M |
| 14 | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N |
| 15 | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O |
| 16 | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P |
| 17 | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q |
| 18 | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R |
| 19 | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S |
| 20 | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T |
| 21 | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U |
| 22 | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V |
| 23 | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W |
| 24 | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | V |
| 25 | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | V | Y |
| 26 | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | V | Y | Z |
Como a palavra-chave do exemplo é composta por nove letras, sendo oito diferentes, durante a encriptação saltas por entre oito linhas diferentes. A vantagem desta cifra é ser impenetrável pela análise de frequências (descrita no artigo anterior). Mas também é bastante mais complicada de utilizar, o que levou a ser ignorada durante mais de dois séculos.
Homem da Máscara de Ferro
Durante este período eram utilizadas cifras monoalfabéticas melhoradas, nas quais as letras eram substituídas por números, por exemplo, de 1 a 100. Dependendo da frequência da letra (em percentagem), esta poderia ter mais do que um número a codificá-la; tratavam-se das cifras homófonas. Um exemplo fantástico é a Grande Cifra de Luis XIV; ele utilizou-a para transmitir mensagens sobre uma das mais intrigantes figuras da época — o Homem da Máscara de Ferro. A cifra fora inventada no séc. XVII por Antoine e Bonaventura Rossignol, pai e filho. Após as suas mortes, perderam-se os pormenores da cifra, impossibilitando o seu estudo.
 Em 1890, foram encontradas, durante umas escavações, cartas
cifradas baseadas nesse método e entregues ao criptoanalista Étienne Bazeries
(1846 - 1931). Após 3 anos de insucessos e frustrações, concluiu que os números
da cifra representavam sílabas. Mas não era tão simples assim, pois a cifra
continha rasteiras; por exemplo, havia números que eliminavam a última sílaba.
Algumas dessas cartas continham informações sobre o Homem da Máscara de Ferro…
Aparentemente tratou-se de um desertor que comprometera toda a campanha
militar, obrigado a ocultar a sua face fora da sua cela, com uma máscara de
ferro. (Porém, outras teorias persistem sobre ser um irmão bastardo de Luís
XIV…)
Em 1890, foram encontradas, durante umas escavações, cartas
cifradas baseadas nesse método e entregues ao criptoanalista Étienne Bazeries
(1846 - 1931). Após 3 anos de insucessos e frustrações, concluiu que os números
da cifra representavam sílabas. Mas não era tão simples assim, pois a cifra
continha rasteiras; por exemplo, havia números que eliminavam a última sílaba.
Algumas dessas cartas continham informações sobre o Homem da Máscara de Ferro…
Aparentemente tratou-se de um desertor que comprometera toda a campanha
militar, obrigado a ocultar a sua face fora da sua cela, com uma máscara de
ferro. (Porém, outras teorias persistem sobre ser um irmão bastardo de Luís
XIV…)
Câmaras Negras
No século XVIII, as cifras monoalfabéticas melhoradas deixaram de ser seguras, pois cada governo tinha uma equipe que se dedicava a decifrar mensagens nas câmaras negras. A mais famosa era a de Viena, Áustria, onde todas as cartas suspeitas enviadas para ou a partir de uma embaixada em Viena eram copiadas, sem ser necessário interromper o seu percurso normal. As cartas forneciam informações importantes aos imperadores da Áustria, e estas eram vendidas a outros países. Só então os criptógrafos adoptaram a cifra de Vigenère.
Telégrafo
A propagação pela Europa em 1851 do telégrafo e o seu código Morse veio revolucionar a Criptografia. Mas os operadores de telégrafo liam sempre a mensagem original, o qual significava muitos problemas de sigilo. A cifra de Vigenère enquadrava-se na perfeição nesta questão, já que a mensagem encriptada não era compreendida pelo operador. Nesta época, esta cifra era considerada inquebrável.
Decifração do Quadrado de Vigenère
O sistema polialfabético de Vigenère resistiu durante 3 séculos, até ao momento em que o matemático britânico Charles Babbage — notavelmente conhecido pelas suas máquinas de diferenças (primitivas máquinas de calcular) — elaborou a teoria de descodificação, em 1854. Mas dado nunca ter publicado a sua descoberta, esta caiu no esquecimento. A descoberta de Babbage foi reconhecida apenas no século XX, quando os seus escritos foram analisados. Mais tarde, Friedrich Kasiski, um oficial reformado do exército prussiano, dedica-se igualmente ao tema, publicando em 1863 no seu livro Die Geheimschriften und die Dechiffrierkunst (As escritas secretas e a arte de decifração) o Teste Kasiski de descodificação das respectivas cifras.
Mas como foi que eles decifraram a técnica de Vigenère?
Tomemos, como exemplo, um texto encriptado com aquela cifra, do qual apenas se conhece o método:
OUPCM EGOEV EYROE OUPCM EGAEX OZVAP GSYWD MUEAU EDOUP
CSQCC APFUC NOCTA FOAOU ZFOQE OYROE VOPGM GFAZE AFQMM
PDAUE YRRQP OHCSC WAXKD MFEEE OZVIZ WAYGN FGVQO OEPOH
KDMFE EFIRG RQPTQ UEYVU PQDMG SBGRM PCMFO YCLRK CMOAE
OASQA EPAXG MNTAZ EAQFO NGMEG AXIUY JOGXE MUSMW DMFEE
QTQOP AEONT EAEHM QDQXE DFEYC NFQQG GJMEO NGRFQ FAKDQ
PEHGF DKAQG MYKMO QNHGR FGEYE HATOA FOOGC MPTAG ARQRM
GSFGM GFADU EOCDM FIMQU FTAYW DMPCM HALFE YQRQU PMPTA
SUQPA AUEYW DMLAO QMAUO UC
Primeiro passo — Descobrir o tamanho da palavra-chave. Para tal, é necessário procurar sequências de letras que apareçam mais do que uma vez no texto em cifra, e a distância entre elas.
Existem duas formas de aparecerem estas sequências: a mesma palavra cifrada várias vezes pela mesma parte da palavra-chave; e duas palavras distintas cifradas utilizando duas partes diferentes da palavra-chave e as quais, por coincidência, têm a mesma sequência de letras no texto em cifra. Se forem procuradas sequências longas, ou seja, com quatro ou mais letras, é aumentada a probabilidade da primeira forma.
O quadro seguinte apresenta grupos de 4 a 6 letras repetidos no texto. Para cada grupo é indicada a sua frequência no texto, assim como a distância entre duas presenças do mesmo grupo. Os restantes valores identificam os factores de espaçamento — os factores multiplicativos dessas distâncias. Por exemplo, a sequência UPCM aparece 2 vezes, separado por 15 letras (contar desde a 1ª letra à 1ª letra seguinte). Os valores de 3, 5 e 15 são os múltiplos dessa distância: (3 x 5) ou (1 x 15).
Quadro 2
| Grupos | freq | dist | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| OUPC | 3 | 42 | * | * | * | * | * | ||||||||||||||
| UPCM | 2 | 15 | * | * | * | ||||||||||||||||
| PCME | 2 | 15 | * | * | * | ||||||||||||||||
| MEG | 2 | 15 | * | * | * | ||||||||||||||||
| YROE | 2 | 60 | * | * | * | * | * | * | * | * | * | ||||||||||
| MEGA | 2 | 183 | * | ||||||||||||||||||
| YWDM | 3 | 336 | * | * | * | * | * | * | * | * | * | ||||||||||
| GMGF | 2 | 240 | * | * | * | * | * | * | * | * | * | * | * | ||||||||
| MGFA | 2 | 240 | * | * | * | * | * | * | * | * | * | * | * | ||||||||
| AZEA | 2 | 111 | * | ||||||||||||||||||
| AUEY | 2 | 273 | * | * | * | ||||||||||||||||
| KDMF | 2 | 27 | * | * | |||||||||||||||||
| DMFE | 3 | 111 | * | ||||||||||||||||||
| MFEE | 3 | 111 | * | ||||||||||||||||||
| MPCM | 2 | 177 | * | ||||||||||||||||||
| MPTA | 2 | 51 | * | * | |||||||||||||||||
| OUPCM | 2 | 15 | * | * | * | ||||||||||||||||
| UPCME | 2 | 15 | * | * | |||||||||||||||||
| PCMEG | 2 | 15 | * | * | * | ||||||||||||||||
| GMGFA | 2 | 240 | * | * | * | * | * | * | * | * | * | * | * | ||||||||
| KDMFE | 2 | 27 | * | * | |||||||||||||||||
| DMFEE | 3 | 111 | * | ||||||||||||||||||
| OUPCME | 2 | 15 | * | * | * | ||||||||||||||||
| UPCMEG | 2 | 15 | * | * | * | ||||||||||||||||
| KDMFEE | 2 | 27 | * | * | |||||||||||||||||
| Total | 6 | 25 | 5 | 12 | 6 | 3 | 4 | 3 | 4 | 0 | 5 | 1 | 2 | 12 | 4 | 1 | 0 | 0 | 4 |
Como facilmente se observa no quadro, o factor multiplicativo mais repetitivo é 3. Logo, assume-se que a palavra-chave é composta por 3 letras.
Segundo passo — Descobrir quais são as letras da palavra-chave. As letras são dadas por L1-L2-L3. Lembra-te que a encriptação começa com a cifra da primeira letra do texto simples, de acordo com a primeira letra da palavra-chave (L1). Para a segunda letra do texto simples foi utilizada L2; para a terceira letra L3. L1, L2 e L3 definem igualmente a linha do Quadrado de Vigenère. Mas atenção: a quarta letra do texto simples é codificada por L1 novamente! Seguindo esta sequência, pode-se considerar que esta cifra polialfabética é constituída por três cifras monoalfabéticas, em que cada uma destas cifras cripta apenas 1/3 mensagem total. Assim, L1 indica o alfabeto a usar para cifrar as 1ª, 4ª, 7ª, 10ª... letras da mensagem. Com esta decomposição, é possível aplicar a análise de frequências ao sistema, mas letra a letra (da palavra-chave), e comparando-as com a frequência do alfabeto português.
O gráfico LP, apresenta a distribuição de frequências-padrão das várias letras na Língua Portuguesa.
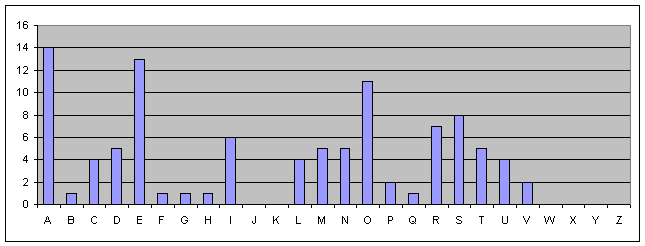
Gráfico LP - Frequências-padrão no Português
Comparando este gráfico com o gráfico L1, este de distribuição de frequências referente a L1, i. é., a frequência de cada letra relativamente às posições 1, 4, 7, etc., é possível prever uma deslocação.
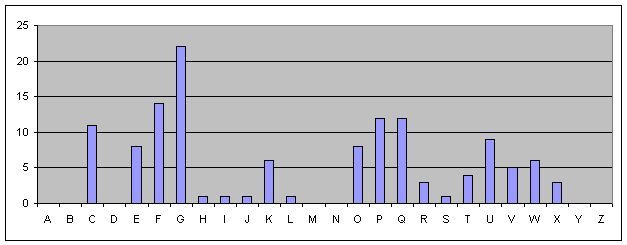
Gráfico L1 - Distribuição de frequências para L1
Assim, as letras R-S-T-U-V no gráfico L1 parecem ter o mesmo comportamento que o P-Q-R-S-T da frequência-padrão (gráfico LP). Também as letras E a K têm aspecto semelhante às C a I da frequência-padrão. Nem todas as letras apresentam um comportamento igual à frequência-padrão: além do texto ser algo curto, não te esqueças que se trata de uma análise estatística.
A análise sugere que todas as letras encriptadas de acordo com L1 foram deslocadas dois lugares. Assim L1 define um alfabeto que começa por C, D, E, F, G… ou seja, L1 será provavelmente C.
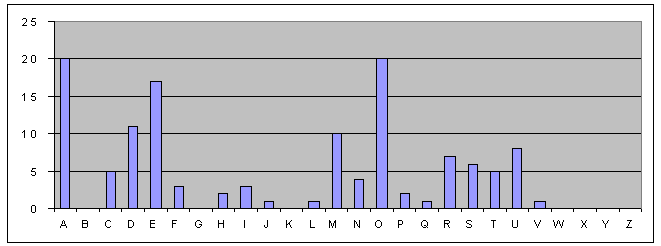
Gráfico L2 - Distribuição de
frequências para L2.
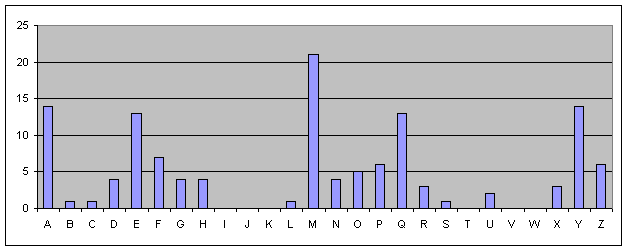
Gráfico L3 - Distribuição de
frequências para L3.
A mesma análise aplica-se a L2 e L3 (vide gráficos L2 e L3). Para L2 não se obtém qualquer deslocação; logo L2 será A. Em L3, o comportamento de M a R é muito semelhante ao de A a F da frequência-padrão. Assim, L3 corresponderá a M.
A potencial palavra-chave está completa: CAM. O Terceiro Passo é agora possível: uma cripto-análise do texto cifra com esta chave, utilizando o Quadrado de Vigenère. Será que a chave está correcta? Ora vamos ver:
Mudam-se os tempos,mudam-se as vontades,
Muda-se o ser, muda-se a confiança;
Todo o mundo écomposto de mudança,
Tomando sempre novasqualidades,
Continuamente vemos novidades,
Diferentes em tudo da esperança;
Do mal ficam as mágoas na lembrança
E do bem (se algum houve) as saudades.
O tempo cobre o chão de verde manto,
Que já coberto foi de neve fria,
E em mim converte em choro o doce canto,
E, afora este mudar-se cada dia,
Outra mudança faz de mor espanto,
Que não se muda já como soía.
Luís de Camões
Livro: O livro dos códigos - Simon Singh – Temas e Debates (1999)